HPO with Genetic Algorithm

Metaheuristics

“meta” = beyond, higher level

“heuristic” = rule of thumb, practical method

Metaheuristics are high-level strategies designed to guide lower-level heuristics to explore the solution space effectively. They are all stochastic algorithms that use randomization and global exploration.

• Randomization provides a good way to move away from the local search to the global search. (i.e. escape local optima)
• It is suitable for non-linear modeling and global optimization.

Goal of using metaheuristics is to find a good enough solution in a reasonable time frame, rather than the optimal solution.

Main components of metaheuristics

1. Intensification (exploitation)
   1. The search in a local region by exploiting the information that a current good solution is found in this region.
   2. It aims to refine and improve the current solution by exploring its neighborhood.
   3. Basically, selecting the best each time converges to a local optimum.
2. Diversification (exploration)
   1. Generates diverse solutions to explore different regions of the solution space.
   2. It helps to avoid premature convergence to local optima by introducing randomness and exploring new areas.
   3. It is important to maintain a balance between intensification and diversification to effectively explore the solution space.

Types of Algorithms

1. Population-based
   1. Maintain and evolve a population of solutions.
   2. Examples: Genetic Algorithms, Particle Swarm Optimization
2. Trajectory-based
   1. Start from a single solution and iteratively improve it.
   2. Examples: Simulated Annealing

Genetic Algorithms (GAs)

Genetic Algorithms (GAs) are a type of population-based metaheuristic inspired by the process of natural selection and genetics. They are used to solve optimization and search problems by mimicking the process of evolution.

Advantages

• GA is gradient-free, making it suitable for non-differentiable, discontinuous, or noisy objective functions.
• GA can be easily parallelized, allowing for efficient exploration of the solution space.
• Different parameters and groups of encoded strings can be manipulated independently, providing flexibility in the search process.

Disadvantages

• Formulation of the fitness function, choosing parameters, determining the selection criteria, and population size can be challenging and may require domain knowledge.

Basic Steps of Genetic Algorithms

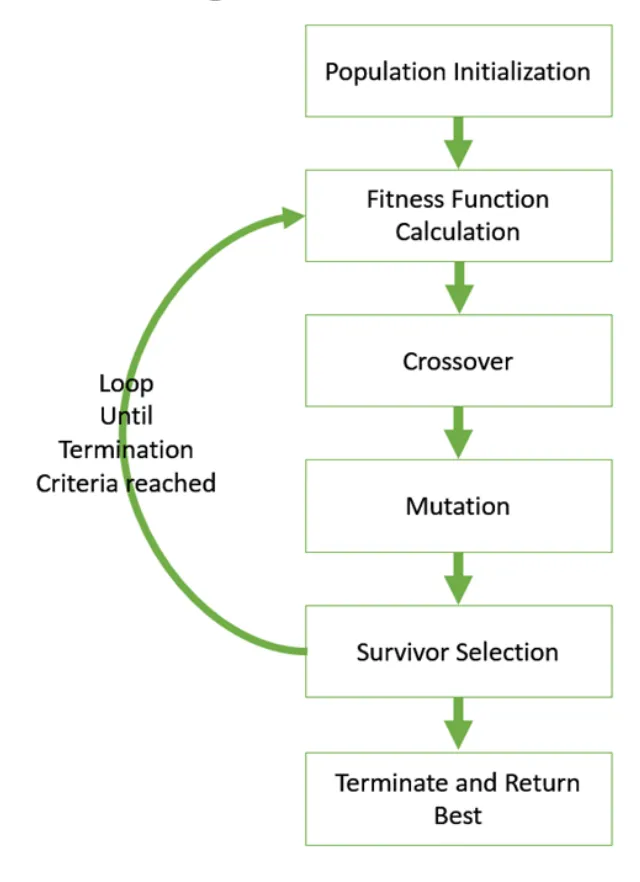
1. Population Initialization
   1. Generate $n$ chromosomes randomly to form the initial population.
   2. $n$ is a hyperparameter that needs to be set. Once set, it remains constant throughout the algorithm.
      1. Too small: May not explore the solution space effectively, leading to premature convergence.
      2. Too large: Increases computational cost and may slow down convergence.
2. Fitness Evaluation
   1. $f(x)$ is the objective function to optimize.
   2. $x$ is a chromosome (solution).
3. Crossover
   1. Select pairs of chromosomes (parents) from the current population based on their fitness scores.
   2. Combine the genes of the parents to create new chromosomes (offspring).

   1
   Parent 1: A B C | D E F
   2
   Parent 2: 1 2 3 | 4 5 6
   3
   Offspring: A B C | 4 5 6
   4
              1 2 3 | D E F

   3. There are many crossover techniques, such as one-point crossover, two-point crossover, and uniform crossover, etc.
4. Mutation
   1. Introduce random changes to the genes of the offspring chromosomes with a low probability (mutation rate).
   2. This helps to maintain genetic diversity and explore new areas of the solution space. It does not happen to every offspring.

   1
    Original: A B C D E F
   2
    Mutated:  A B X D E F

5. Survivor Selection
   1. Population size must remain constant, so we need to select which chromosomes will survive to the next generation.
   2. Common strategies include:
      1. Generational Replacement: Replace the entire population with the new offspring.
      2. Elitism: Retain a few of the best chromosomes from the current population and fill the rest with new offspring.
   3. Go back to step 2 and repeat until a stopping criterion is met.
6. Termination
   1. The algorithm stops when a predefined stopping criterion is met, such as reaching a maximum number of generations or achieving a satisfactory fitness level.

Example Hyperparameter Optimization with GAs

Given Problem:

Use the following assumptions to generate the dataset:

• True model: $y = 2x + 1$
• $x$: Generate 100 random $x$ values.
• $y$: Generate 100 $y$ values with the above $x$ and add error with a normal distribution.
  • e.g. $y = 2x + 1 + \text{error}$
• Use the same loss function on the upper and lower level.
  • Ridge regression loss: $\Sigma (y - \hat{y})^2 + \lambda \times m^2, \text{where} \space \hat{y} = mx + b$

Steps to solve:

1. Write lower level optimization problem
2. Write Upper Level evaluation
3. Genetic Algorithm HPO
4. Test

1
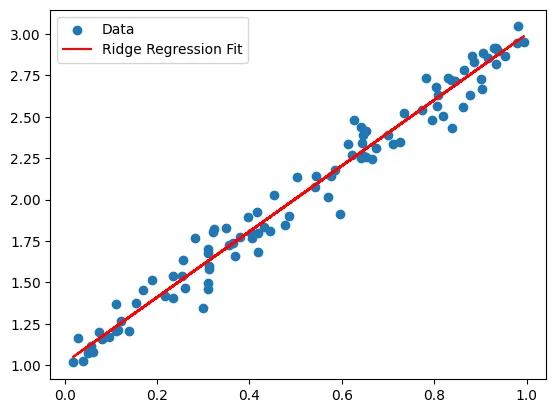
import numpy as np
2
from sklearn.linear_model import Ridge
3
from sklearn.model_selection import train_test_split
4
import matplotlib.pyplot as plt
5
import random
6

7

8
# Generate Data
9
x = np.random.rand(100)
10
y = 2 * x + 1 + np.random.normal(0, 0.1, 100)
11

12
# Split Data
13
X_train, X_val, y_train, y_val = train_test_split(x.reshape(-1, 1), y, test_size=0.2, random_state=42)
14

15

16
# Lower Level Optimization
17
def lower_opt(X_train, y_train, lambda_):
18
    model = Ridge(alpha=lambda_)
19
    model.fit(X_train, y_train)
20

21
    m = model.coef_[0]
22
    b = model.intercept_
23
    return m, b
24

25

26
# Upper Level Evaluation
27
def upper_eval(X_val, y_val, m, b, lambda_):
28
    obj = np.sum((y_val - (m * X_val.flatten() + b)) ** 2) + lambda_ * (m ** 2)
29
    return obj
30

31

32
# Genetic Algorithm HPO
33
def genetic_algorithm_hpo(X_train, y_train, X_val, y_val, pop_size, num_generations, mutation_rate, crossover_rate):
34
    # Step 1: Initialize Population
35
    population = [random.uniform(0, 1) for _ in range(pop_size)]
36

37
    # Generation
38
    for generation in range(num_generations):
39
        # Step 2: Evaluate Fitness
40
        fitness_scores = []
41
        for lambda_ in population:
42
            m, b = lower_opt(X_train, y_train, lambda_)
43
            fitness = upper_eval(X_val, y_val, m, b, lambda_)
44
            fitness_scores.append(fitness)
45

46
        # Step 3: Selection (Tournament Selection) - Select the best half --> exploitation
47
        selected_parents = [population[i] for i in np.argsort(fitness_scores)[:pop_size // 2]]
48

49
        new_population = selected_parents.copy()
50
        while len(new_population) < pop_size:
51
            # Step 4: Crossover --> exploration
52
            if random.random() < crossover_rate:
53
                parent1, parent2 = random.sample(selected_parents, 2)
54
                child = 0.5 * parent1 + 0.5 * parent2
55
            else:
56
                child = random.choice(selected_parents)
57

58
            # Step 5: Mutation
59
            if random.random() < mutation_rate:
60
                child += random.uniform(-0.1, 0.1)
61
                child = min(max(child, 0.0001), 1)
62

63
            new_population.append(child)
64

65
        population = new_population  # update population each generation
66

67
    # Recalculate fitness for final population
68
    fitness_scores = []
69
    for lambda_ in population:
70
        m, b = lower_opt(X_train, y_train, lambda_)
71
        fitness = upper_eval(X_val, y_val, m, b, lambda_)
72
        fitness_scores.append(fitness)
73

74
    best_lambda = population[np.argmin(fitness_scores)]
75
    return best_lambda
76

77

78
# Run Genetic Algorithm
79
best_lambda = genetic_algorithm_hpo(X_train, y_train, X_val, y_val, pop_size=20, num_generations=50,
80
                                    mutation_rate=0.1, crossover_rate=0.7)
81

82
# Check Final Model
83
final_model = Ridge(alpha=best_lambda)
84
final_model.fit(X_train, y_train)
85

86
# Plot Results
87
plt.scatter(x, y, label='Data')
88
plt.plot(x, final_model.coef_ * x + final_model.intercept_, color='red', label='Ridge Regression Fit')
89
plt.legend()
90
plt.show()